In this final post of the three-part serie, I will describe different algorithms that exist for the Multi-Objectives Shortest Path problem and how it applies to the multi-transfers flight routes explained in the previous post. I also came up with a simple but understandable algorithm to this problem. Before describing the algorithms, let's have an overview of what are done in this field by looking at some of the state of the art. Also, popular algorithms such Dijkstra, Bellman-Ford, and A*(http://A* search algorithm) (pronounced as "A star") are only suitable for Single-Objective Shortest Path. The following techniques applies for problems with multiple weights to optimize.

Scalarization technique

Since Dijkstra's algorithm only works for shortest path involving a single objective, one of the method that is used, is the scalarization technique. This method consists of combining multiple objectives into a single objective scalarization function. This method, often known as weighted-sum method, basically, we choose a function which transforms the vector weights into scalar weights. Consequently, the problem turns into a single objective optimization and one can apply algorithm like Dijkstra's algorithm. If all objectives are additional, for instance, the total duration of flights within a trip, it's called linear weighted-sum. We can express the new cost function which is a linear combination of multiples objections functions as:

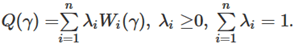
But in case of objectives functions that cannot be combined in a linear way, such as an indice that represents how a segment of a path is dangerous, we should instead consider the maximum value which is representative of the entire path. The new single objective function:

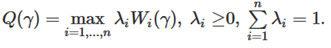
Epsilon-constraint method

Instead of combining multiples objectives into a single cost function, there are other methods that are used to find shortest path by keeping all criterion as they are. The epsilon-constraint method, consists of letting the decision maker chooses a specific objective out of all the objectives to be minimized, and the other remaining objectives values have to be less than or equal to a given epsilon value. Each remaining objective has its own epsilon constraint value. Mathematically, it can be express as:

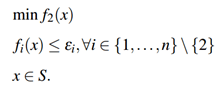
The advantage of this method is that it lets the decision maker to choose which objective to minimize. In our case, a business traveler for instance, might prioritize the flight duration over the price, whereas the casual traveler might want to minimize the price.

As opposed to the scalarization technique, this method doesn't require to find a new cost function which combines all objectives functions. The epsilon-constraint method is quite useful when the optimization problem has a lot of objectives. The following figure illustrates the epsilon-constraint method with two objectives f1 and f2.

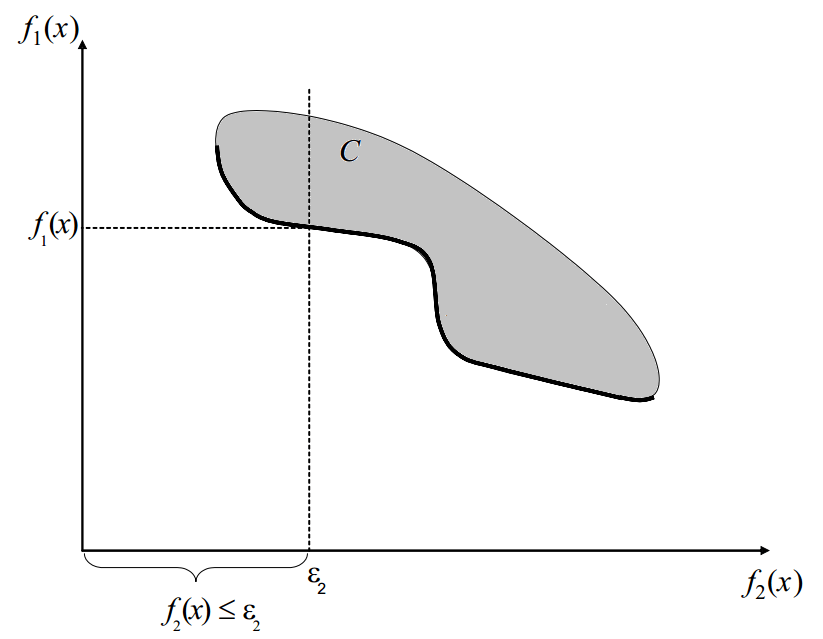
Figure 1 - Epsilon-constraint method for two objectives functions f1 and f2

Pareto efficiency and Skyline Path

Non-dominated solution

In Multi-Objective optimization, the Pareto optimization[6] consists of finding a subset of solutions, called non dominated solutions. For instance, in the case where there are two objectives functions, a solution s1 can be said to dominate another solution s2 if the cost (f1,g2) of s1 better than the cost (f2,g2) in the Pareto sense if:

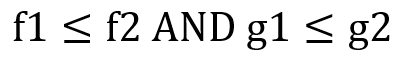
with one of the inequalities being strict. In a more general way, with more than two objectives this can be express as the following:

With d being the total number of objectives, a cost vector a, in the space of d-dimension real vector space, dominates another cost vector b, if a has a smaller cost value than b in at least one dimension i and b does not have a smaller cost value than b in any dimension j such as:

Pareto front or Skyline Path

Pareto front, or more commonly called Skyline Path, is the set of all the non-dominated paths from a source node S to a specific destination D.

The following figure illustrates the concept of Skyline Path.

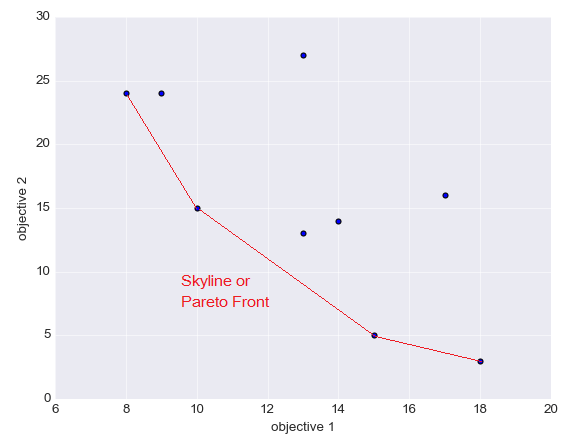
Figure 2 - Pareto front or Skyline Path illustration

This method assures that all solutions in the Pareto front are not dominated but any other solution. It's then up to the decision maker to choose between these Pareto optimal solutions. For instance, if s/he would rather prefer minimizing the objective 1, then the Pareto optimal on the left upper side would be preferred. This makes sure that in addition of the minimization of the objective 1, the chosen solution also has a minimum value in regard to the objective 2.

Implementation of Multi-Objectives Shortest Paths Algorithms

In the previous post I managed to design a model for connecting flights with multiple transfers and this model is satisfying enough in term of query time and easy to do further analysis. In this section, I will discuss about how to find valid trips that contain connectible routes in term of departure and arrival time. A natural way to define a valid trip, is that, the trip only contains connecting flights that satisfies the chronological order of the arrival time of the segment n and the departure time of the segment n+1.

Analyzing the query result

The first step before writing any algorithm is to analyze the result returned by the Cypher query. The Web UI of Neo4j only allows a visualization of the result and becomes quickly visually overwhelmed when the result contains lots of nodes and relationships. Therefore, I am going to use py2neo, which is a Python client library and toolkit for working with Neo4j.

The result returned by the Cypher query is a Cursor, which is a navigator for a stream of records. Simply put, it acts like an iterator. The Cypher query returns the pattern as paths. Each path is a walkable, that is, a subgraph with added traversal information such as nodes and relationships properties. I then extract all the nodes and relationships from each path.

The result can also be consumed and extracted entirely as a list of Python dictionaries.

The final two objectives to optimize is:

• The price, which is an explicit weight on the Neo4j model and is actually one of the properties of the relationship that links two airports nodes.
• The duration, which is computed after designing the Neo4j model, represents the duration of flight segment and transfer time.

Finding all simple paths

The first attempt to analyze the result returned by the Cypher query is to load the result into a NetworkX multi-edges directional graph, since it already includes convenient built-in algorithms such as finding all simple paths, that is, paths which traverse only a node once. By design, Neo4j finds paths using pattern, and the result returned by the query might include paths with a same node traversed more than once as long as the traversed relationships are different. Unfortunately, NetworkX's all simple paths algorithm only provide for each simple path, the nodes data and not the edges data (=relationships properties). After a few attempt in vain to modify the built-in algorithm, I proceed with another method.

I could try to write my own all simple paths searching algorithm, which uses a Depth-First Search, but fortunately, the Neo4j 3.0 introduced the concept of user defined procedures under the name of APOC (Awesome Procedures On Cypher). These are implementation of certain functionally not easily expressed in Cypher, including for example data integration/conversion and graph algorithm. After adding the APOC library in the Neo4j plugin, we can start using it by calling the CALL clause. In my valid routes searching algorithm, I am going to use the APOC's allSimplePaths function. The function requires a maxNodes parameter that specifies the number of maximum nodes we want to have in the paths, in our problem, this is related to the number of transfers. The Cypher query looks something like:

MATCH (m:Month{month:{month}})-[:HAS_DAY]->(d:Day{day:{day}})-[:HAS_AIRPORT]->(s:Airport{airportName:{origin}})
MATCH (t:Airport{airportName:{destination}, month:{month}, day:{day}})
WITH m,d,s,t
call apoc.algo.allSimplePaths(s,t,'>',{maxNodes})
YIELD path as p
RETURN nodes(p) as nodes, relationships(p) as rels limit {limit_routes_count}

Finding valid routes

The following figure illustrates an example of a trip:

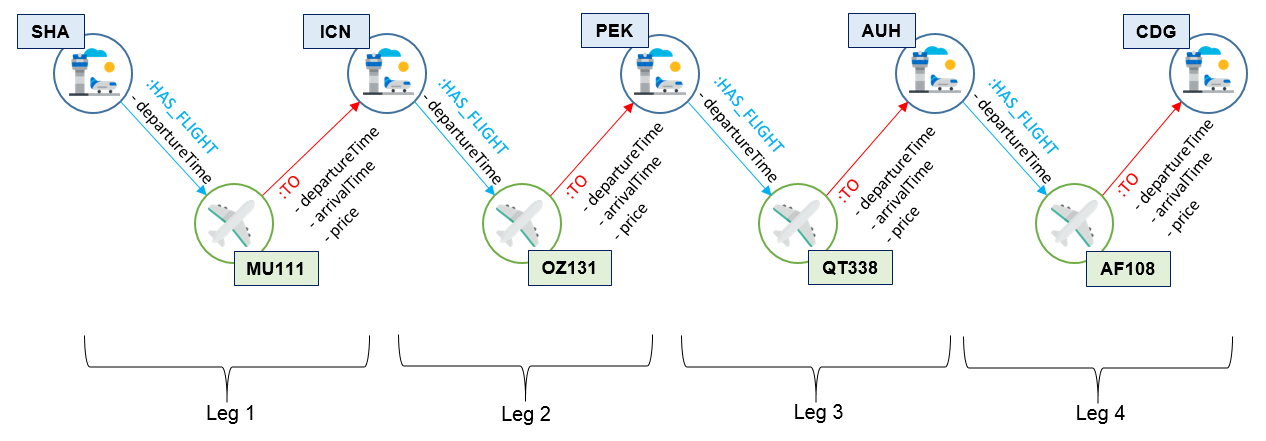
Figure 3 - Example of a 3-stops trip, illustrating nodes and relationships connections

A trip is valid, if this trip contains connecting flights that satisfies the following conditions:

• The first segment departure month and day is identical to the ones specified by the query. This allow to immediately stop the algorithm before doing further processing.
• All the flight legs in the trip contains the same departure time in both relationships (HAS_FLIGHT and TO) connecting the flight node to the source and target airports nodes.
• Between two legs, the departure time d in the HASFLIGHT relationship of the leg _n+1, and the arrival time a in the TO relationships of the leg n verifies: d - a > min_transferTime, where min_transferTime is the minimum duration for the transit (in minute). I choose 30 for this value, which means that a trip which contains transits whose waiting time is less than 30 minutes is considered as invalid trip. This minimum transfer time gives the traveler enough time to reach their next flight.

I am going to iterate through each walkable object returned by the Cypher query, and extract the subgraph information as two lists: a list nodes_list of all the nodes (and their properties) constituting the path and a list rels_list of all the relationships (and their properties) that link the nodes constituting the path.

The following is a pseudo-code of the algorithm, which has a time complexity of O(l*w), where l is the number set by the query limit and w is length of a walkable.

while(cursor.forward()):
  isValidRoute = list()
  for i in range(0, len(rels_list), step=2): # i step is 2 because we consider pair of only (HAS_FLIGHT->TO) and not (TO->HAS_FLIGHT)
    if departure_month==month and departure_day==day: # if the first HAS_FLIGHT is departing on the same day specified
      haveSameDepartime = rels_list[i]['departure_time'] == rels_list[i+1]['departure_time']
      j = i + 1
      if not haveSameDepartime: # Invalid route: contains segments dont have the same departure_time for :HAS_FLIGHT and :TO
        isValidRoute.append(False)
        break # quit the for loop, move to next walkable
      else:
        if len(rels_list)==2: # if non stop trip
          appendFlightInfo(price, duration)
          isValidRoute.append(True)
        else: # at least 1 stop route
          try:
            leg_2_departure_time = rels_list[j+1]['departure_time']
            leg_1_arrival_time   = rels_list[j]['arrival_time']
            transfer_time  = leg_2_departure_time - leg_1_arrival_time
            if (transfer_time > 30): # if the following flight is later than the arrival and the waiting time is > 30min
              transfer_time_list.append(transfer_time)
              appendFlightInfo(price, duration)
              isValidRoute.append(True)
            else: # Invalid route: contains segments with departure time earlier than arrival time.
              isValidRoute.append(False)
              break
          except IndexError: # target reached, ie: end of leg segment nodes reached, IndexError coz i move increases 2 by 2
            appendFlightInfo(price, duration) # to get the last duration and price in the last :TO relationship

    else: # Invalid trip: flight departure day doesnt match the specified day.
      isValidRoute.append(False)
      break

  if all(isValidRoute):
    extractFlightsInfo()

Once I manage to extract all the valid trips, I use Pandas library to convert the nodes and relationships properties in an easily understandable way and then convert them into a .CSV file. This file contains now in addition to a correct chronological order for the departure and arrival time; airports name; a list of all the price, the flight duration, transfer time, the number of transfer counts.

Note: the APOC's allSimplePaths function behaves in the way that all paths with a total number of nodes close to the maxNodes are fetched in priority. For instance, of we set , most of the results returned by the query are paths (valid and invalid) that contain 8 nodes (airports and flights nodes) which corresponds to 3-stops trips. Therefore we either specify a great number of  (like 10) to fetch 0, 1, 2, 3 or 4 stops trips and a great number of the result limit (like 200 000), but this will increase greatly the query time. Therefore, I decide to set different value for the maxNodes parameter to fetch separately, 0, 1, 2, 3 and 4 stops trips and then combine the results by deleting duplicating valid trips. This also ensure that we fetch all the possible trips with different number of transfers.

We can now proceed to the optimization of the price and duration objectives.

Optimizing the price and duration objectives

Skyline Path algorithm

The Skyline Path (Pareto front) algorithm is quiet a well-known algorithm, and a Python implementation can be found in Matthew Woodruff's GitHub inspired by K. Deb's papers.

The result of this algorithm is not satisfying enough because the profile of the distribution of the total price and total duration doesn't have a clearly defined Pareto front. Moreover, Matthew's algorithm won't let choosing a "top-ranked" solutions. Therefore, I decide to implement my own algorithm which fit better the profile of the distribution of both objectives.

"Max alpha" Algorithm

I have thought of an algorithm that would find all top-ranked optimal solutions. Here, the optimal solution would be solutions that are close to the best solution possible, which would be the solution that has the lowest price and duration, so optimize both the price and the duration. Of course, this best solution possible might exist or not, and we define this solution by associating the vector of optimal cost which is:

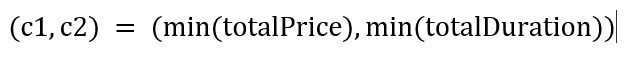
The minimum of the total price and total duration are found within values in the solutions (=valid trips). I then, for each solution s in the set of all solutions S, calculate the value of alpha, that verifies:

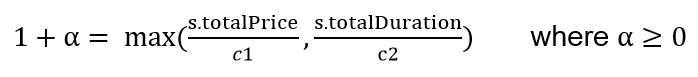
The goal is to rank solutions based on their value of alpha, which represent in some way, the "distance" to the best solution possible. The smaller the value of alpha, the better the solution is. I choose the maximum of the ratio between the given solution price and duration because, the maximum of both is representative of the fact that this objective "penalize “the given solution.

The following figure shows the top 100 optimal solutions found by this algorithm.

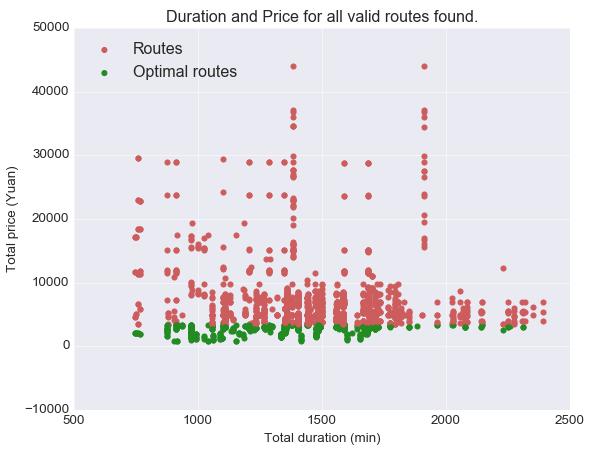
Figure 4 - Optimal solutions with the "max alpha" method

The problem with this algorithm is that it favors solutions with low total duration, since the range of the total duration is smaller than the total price's one. Therefore, the maximum in the alpha expression will most of the time be the total price ratio, so the value of alpha will be great.

Euclidean distance-based Algorithm

Instead of calculating alpha, we use the Euclidean distance between a given solution to the best solution possible. The vector used to compute this distance is of course the vector composed by the total price and total duration. Here's the result:

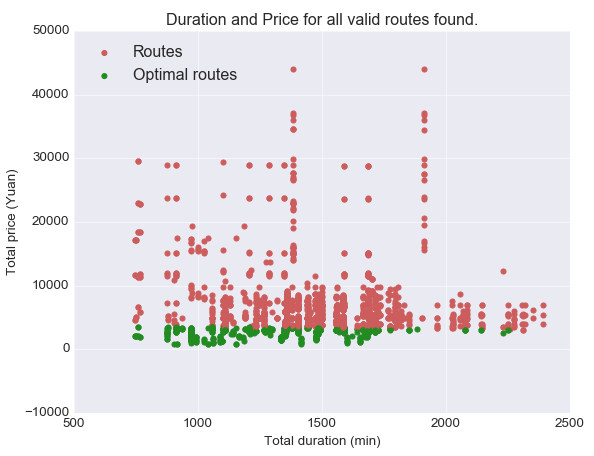
Figure 5 - Optimal solutions with the Euclidean distance-based method

Unfortunately, this method, similarly to the previous one, favors solutions with low price for the same reason. What we would like to obtain is solutions that are not favored by a specific objective due to its distribution, but both objectives, regardless their range.

Mahalanobis distance-based Algorithm

The idea to address the problem in the previous algorithm, is not to "bias" against a particular objective. We would like somehow to "standardize" all the objectives. This is where the Mahalanobis distance helps. Simply put, the Mahalanobis distance is a generalized version of the Euclidean distance, and is somehow a "weighted Euclidean distance". It basically "normalizes" all the components in the vector. The rigorous definition is described in here, for this project, I am going to use the implementation of this metric which is include in the Python's Scipy library. Especially the cdist function is used and the metric parameter is set to Mahalanobis. The following figure shows the result of the method:

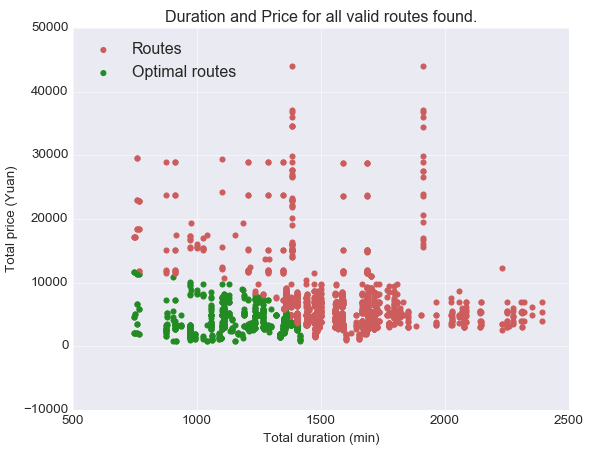
Figure 6 - Optimal solutions with the Mahalanobis distance-based method: none of the objectives are biased

With this method, I manage to find a ranked subset of optimal solutions, that take into account both the total price and total duration objectives. Once the ranked optimal solutions found, I have written a function using Python’s Pandas to retrieve flights information related to these optimal solutions. This method can also be applied for more than two objectives optimization problem.

Conclusion

In this project divided into a serie of three part, I explained how to fully design from scratch a model for multiple transfers flight routes, using different technologies and implementing original algorithms for the Multi-Objective Shortest Paths problems. This implementation is scalable and easy to follow. The difficult parts include, amongst others, designing different models that lead steadily to a final and satisfying model and always seeking for the best performance in term of query time.

The starting point was a mere dataset file, and before being able to start thinking of any algorithms, different steps are required, such as cleaning the dataset, migrating to a different but more suitable type of database, turning the problem into a graph searching problem etc.

For the complete code, please check my GitHub repository.